Pathfinding en Neo4J

Soyons honnêtes, nous nous sommes tous déjà perdu dans le métro parisien. C’est pourquoi nous allons aujourd’hui créer notre propre système d’itinéraire pour lignes de métro. En effet, aujourd’hui nous allons explorer un peu plus en détail le pathfinding en Neo4J et à quel point il y a possibilité de faire des queries puissantes assez simplement.

Ce tutoriel s’adresse à des gens connaissant déjà la base de la syntaxe de Neo4J, si ce n’est pas votre cas je vous conseille de commencer par la base. Si c’est votre cas ou que vous êtes ici uniquement par curiosité, nous allons voir comment avec quelques fonctions un peu plus poussées nous pouvons faire de grandes choses. Alors sortez votre pass Navigo, et embarquons !

Créer son métro

Pour des questions évidente de « c’est trop long », nous n’allons nous contenter ici que de quatre lignes de métro. Créez-les dans cet ordre:

//Create metro 14
CREATE (:Station {name: "Olympiades"})-[:CONNECTED {line:"14", duration: 2}]->(:Station {name: "Bibliothèque François Mitterand"})-[:CONNECTED {line:"14", duration: 2}]->(:Station {name: "Cour St-Emilion"})-[:CONNECTED {line:"14", duration: 1}]->(:Station {name: "Bercy"})-[:CONNECTED {line:"14", duration: 2}]->(:Station {name: "Gare de Lyon"})-[:CONNECTED {line:"14", duration: 3}]->(:Station {name: "Chatelet"})-[:CONNECTED {line:"14", duration: 2}]->(:Station {name: "Pyramides"})-[:CONNECTED {line:"14", duration: 2}]->(:Station {name: "Madeleine"})-[:CONNECTED {line:"14", duration: 1}]->(:Station {name: "Saint Lazare"})

//Create metro 5
CREATE (:Station {name: "Place d'Italie"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Campo Formio"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Saint Marcel"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Gare d'Austerlitz"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Quai de la rapée"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Bastille"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Bréguet Sabin"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Richard Lenoir"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Oberkampf"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"République"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Jacques Bonsergent"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Gare de l'Est"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Gare du Nord"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Stalingrad"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Jaurès"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Laumière"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Ourcq"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Porte de Pantin"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Hoche"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Église de Pantin"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Bobigny-Pantin Raymond Queneau"})-[:CONNECTED {line:"5", duration: 1}]->(:Station {name:"Bobigny Pablo Picasso"})

//Create metro 6
MATCH (bercy:Station {name:"Bercy"}), (italie:Station {name: "Place d'Italie"})
CREATE (:Station {name:"Nation"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Picpus"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Bel-Air"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Daumesnil"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Dugommier"})-[:CONNECTED {line:"6", duration:1}]->(bercy)-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Quai de la Gare"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Chevaleret"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Nationale"})-[:CONNECTED {line:"6", duration:1}]->(italie)-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Corvisart"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Glacière"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Saint-Jacques"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Denfert Rochereau"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Raspail"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Edgar Quinet"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Pasteur"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Sèvres Lecourbe"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Cambronne"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "La Motte Picquet Grenelle"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Dupleix"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Bir Hakeim"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Passy"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Trocadero"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Boissière"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Kléber"})-[:CONNECTED {line:"6", duration:1}]->(:Station {name: "Charles de Gaulle Étoile"})

//Create metro 2
MATCH (nation:Station {name:"Nation"}), (jaures:Station {name: "Jaurès"}), (stalingrad:Station {name: "Stalingrad"}), (cdg:Station {name: "Charles de Gaulle Étoile"})
CREATE (nation)-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Avron"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Alexandre Dumas"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Phillipe Auguste"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Père Lachaise"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Menilmontant"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Couronnes"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Belleville"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Colonel Fabien"})-[:CONNECTED {line:"2", duration:1}]->(jaures)-[:CONNECTED {line:"2", duration:1}]->(stalingrad)-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "La Chapelle"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Barbès rochechouart"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Anvers"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Pigalle"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Blanche"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Place de Clichy"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Rome"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Villiers"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Monceau"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Courcelles"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Ternes"})-[:CONNECTED {line:"2", duration:1}]->(cdg)-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Victor Hugo"})-[:CONNECTED {line:"2", duration:1}]->(:Station {name: "Porte Dauphine"})

Une fois cela fait, vous obtiendrez normalement un résultat similaire:

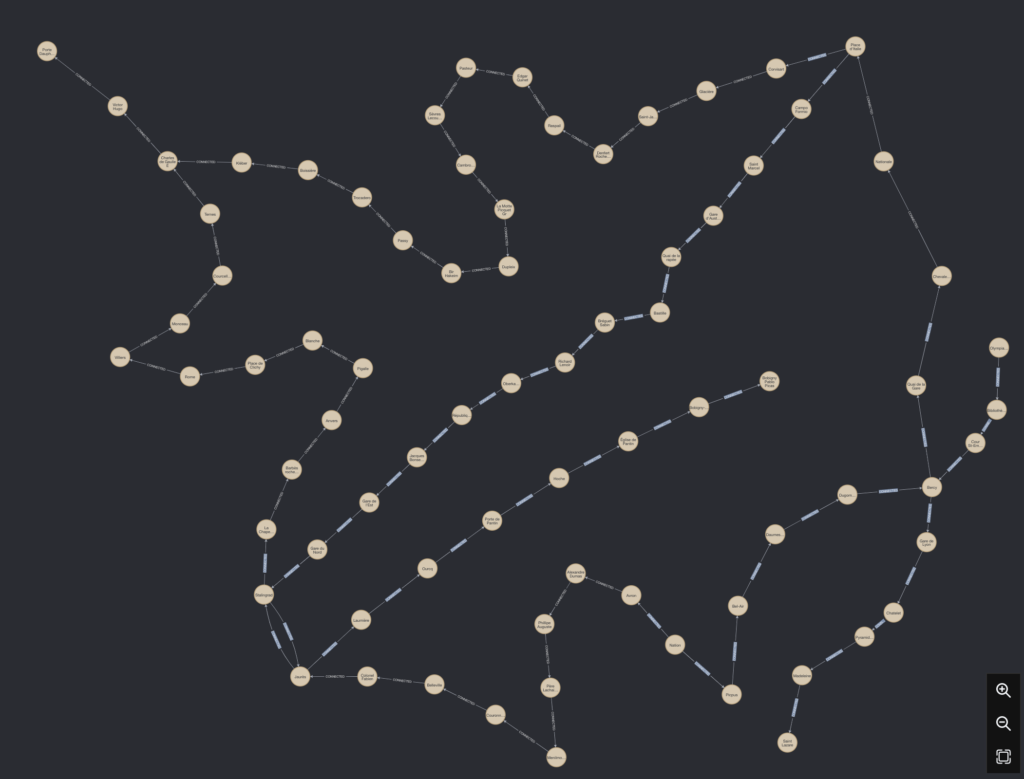
Ici les noeuds représentent les stations physiques et les relations la ligne qui les relie. Par exemple Gare du Nord et Gare de l’Est sont reliées entre elles à la fois par la ligne 4 et la ligne 5, on y verrait donc deux relations si nous avions la ligne 4. Sur chaque relation vous verrez donc le numéro de ligne ainsi que la durée du trajet entre ces deux stations.

Base de notre Pathfinding

Nous allons donc ici devoir trouver déjà le chemin le plus court entre deux stations. Pour ce faire, rien de plus simple:

MATCH p=shortestPath((:Station{name:"Belleville"})-[*]-(:Station{name:"Stalingrad"})) RETURN p

Ici la syntaxe vous parlera normalement. Nous commençons avec le mot clé « MATCH » pour indiquer que nous allons chercher un pattern. Ensuite, nous appelons la fonction shortestPath() avec comme paramètre les deux stations que nous voulons traverser reliées par une relation de taille infinie (indiquée par l’étoile). Puis nous retournons ce que cette fonction retourne. Notez que le « :Station » est optionnel étant donné que nous n’avons ici que des stations, mais cela permet de rajouter d’autres labels par la suite si besoin.

Vous obtiendrez alors ceci:

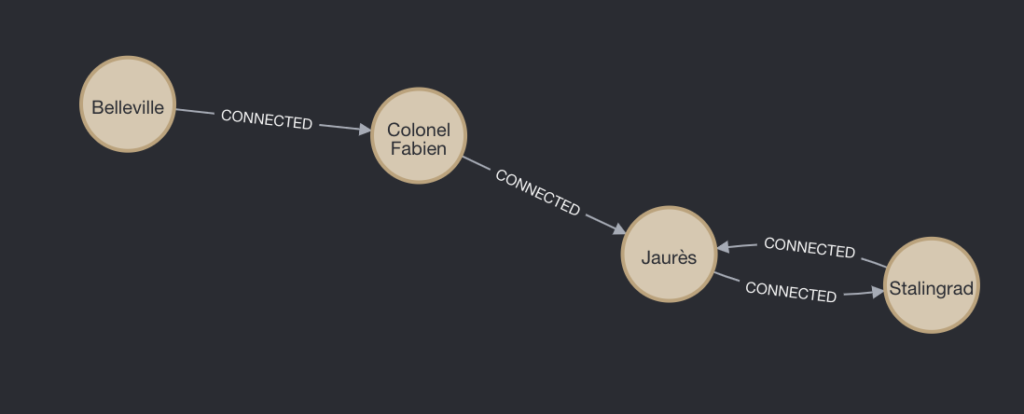
Allons plus loin

Maintenant que nous savons comment simplement trouver notre itinéraire nous voulons savoir combien de temps cela nous prendrait. Pour ça, nous allons utiliser la propriété « duration » présente sur nos relations. Nous allons donc devoir boucler sur les relations de notre path et additionner toutes les durations que nous avons.

Notons un point intéressant ici: entre Jaurès et Stalingrad nous avons deux relations. Si on comptait les durations des relations affichées ici nous aurions une erreur. Il faut cependant distinguer les résultats affichés et les résultats retournés. Le moteur graphique de Neo4J vous affichera même les relations que vous ne demandez pas à retourner. Le fait d’avoir ici trois relations au lieu de quatre ne pose donc pas de soucis pour cet exercice.

Au niveau des étapes nécessaires, nous devons déjà récupérer notre path, puis récupérer toutes les relations et enfin additionner toutes les durations que nous avons pour retourner le résultat. Commençons donc par la récupération des relations, pour cela une fois n’est pas coutume: nous avons une fonction toute faite en Neo4J. La fonction RELATIONSHIPS(). Cette fonction retournera automatiquement un array de relations quand on lui donne un path en paramètre.

Ensuite nous devons boucler sur nos relations pour récupérer la durée totale, pour cela Neo4J dispose comme beaucoup d’autres langages d’une fonction reduce(). Cette fonction va fonctionner en trois étapes: déclarer une variable qui sera retournée, donner l’array à boucler puis donner la syntaxe à effectuer. Elle se découpe comme ceci:

reduce(variable=0, item IN array | variable + item.property)

Pour notre exercice nous allons donc pouvoir l’écrire de la façon suivante:

reduce(t=0, r IN RELATIONSHIPS(p) | t+r.duration)

Cependant, si nous écrivons ceci dans notre return, la clé retournée ne sera pas très pratique pour faire une API propre (voir en haut à droite):

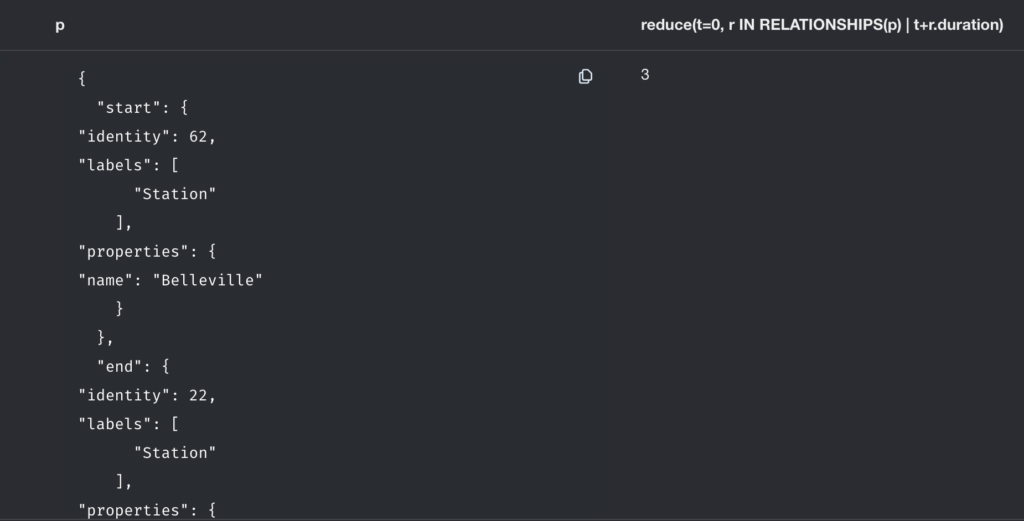
Nous allons donc, comme en SQL, préciser la clé sous laquelle nous voulons retourner ce résultat avec un AS:

MATCH p=shortestPath((:Station{name:"Belleville"})-[*]-(:Station{name:"Stalingrad"}))
RETURN p, reduce(t=0, r IN RELATIONSHIPS(p) | t+r.duration) AS time

Quid des stations fermées ?

Et oui, quiconque a déjà pris le métro s’est sans doute déjà confronté à ce soucis: une station parisienne, ça ferme facilement. Travaux, soucis, les causes sont nombreuses. Nous allons donc pour cela adapter notre système. Premièrement: fermons une station. S’il y a des travaux à Gare du Nord, elle ne ferme pas forcément toutes les connexions, mais plutôt simplement un quai. Donc en cas de travaux c’est par exemple juste la connexion de la ligne 4 qui sera fermée entre la Gare du Nord et la Gare de l’Est. Nous allons donc ajouter un {closed: true} sur une relation.

MATCH (:Station{name:"Colonel Fabien"})-[r]-(:Station{name:"Jaurès"})
SET r.closed=TRUE
RETURN r

Désormais, nous ne pouvons plus prendre notre chemin direct. Mais quel est donc l’itinéraire le plus rapide désormais ? Nous allons chercher ça !

Pour ajouter une condition à notre recherche, nous allons évidemment passer par un WHERE. Nous devons ensuite vérifier qu’aucune de nos relations n’ait de i.closed = true. Cependant, toutes nos relations n’ont pas de i.closed, donc pour éviter des erreurs nous allons déjà vérifier que la propriété existe.

Pour vérifier une condition sur une large quantité d’entités (noeuds ou relations) nous avons deux fonctions: ALL et NONE. Etant donné que nous ne voulons qu’aucune de nos relations n’ait ce i.closed, nous allons donc passer par un NONE. La syntaxe va donc s’écrire comme suit:

MATCH p=shortestPath((:Station{name:"Belleville"})-[*]-(:Station{name:"Stalingrad"})) 
WHERE NONE(i IN RELATIONSHIPS(p) WHERE EXISTS(i.closed) AND i.closed=TRUE)
RETURN p, reduce(t=0, r IN RELATIONSHIPS(p) | t+r.duration) AS time

Ici avant notre return nous précisons qu’aucune de nos relations ne doit avoir un i.closed à true si il existe dans la relation. Après cela, nous laissons notre query s’effectuer comme avant, et nous obtenons désormais un résultat de 29 minutes pour tout ce trajet (donc mieux vaut le faire à pied).

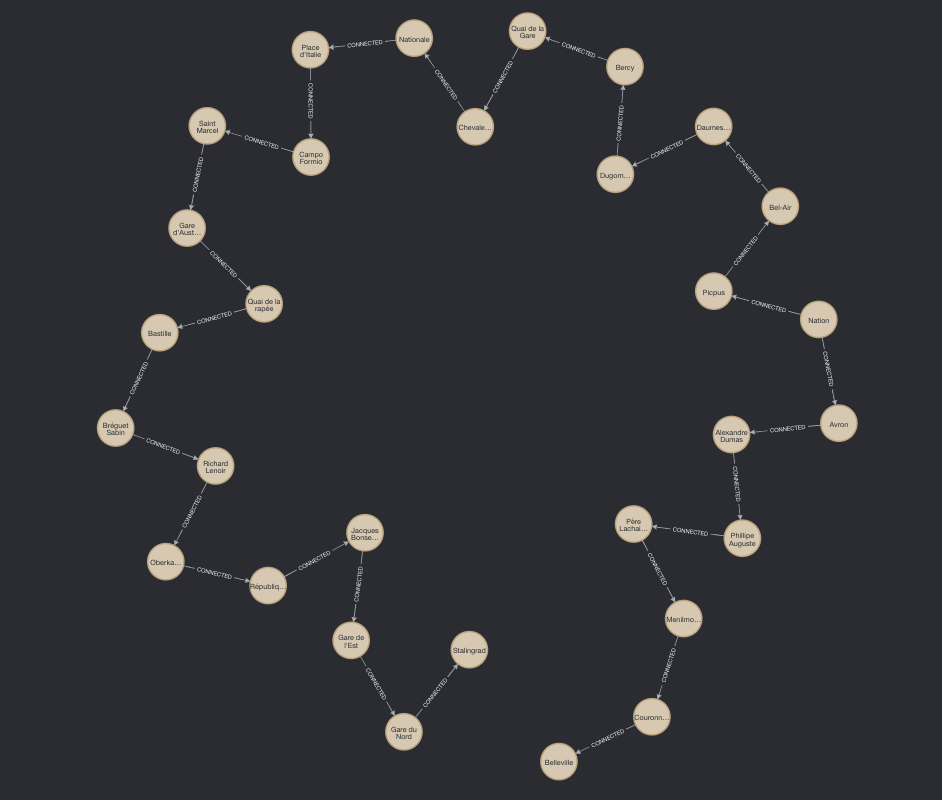
Et voilà

Nous avons désormais notre système prêt à l’emploi avec possibilité de préciser quand une station se ferme ou réouvre. Maintenant, si vous êtes braves, je vous met au défi de vous lancer dans le même projet en utilisant du SQL !
Blague à part, cet exercice est intéressant pour démontrer la puissance des bases de donnée orientées graphe dans ce type de projet. Évidemment ce type de base de données n’est pas efficace en toute situation. À chacun de faire ses choix en fonction du projet, de ses compétences et de ses préférences.